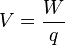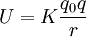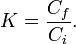Fisica
miércoles, 8 de diciembre de 2010
Energia potencial y trabajo electrico
Trabajo eléctrico y energía potencial eléctrica
Considérese una carga puntual q en presencia de un campo eléctrico. La carga experimentará una fuerza eléctrica. Se define como el trabajo "W"
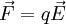
Ahora bien, si se pretende mantener la partícula en equilibrio, o desplazarla a velocidad constante, se requiere de una fuerza que contrarreste el efecto de la generada por el campo eléctrico. Esta fuerza deberá tener la misma magnitud que la primera, pero sentido contrario, es decir:
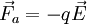 (1)
(1) Partiendo de la definición clásica de trabajo, en este caso se realizará un trabajo para trasladar la carga de un punto a otro.De tal forma que al producirse un pequeño desplazamiento dl se generará un trabajo dW. Es importante resaltar que el trabajo será positivo o negativo dependiendo de cómo se realice el desplazamiento en relación con la fuerza 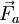 . El trabajo queda, entonces, expresado como:
. El trabajo queda, entonces, expresado como:

Nótese que en el caso de que la fuerza no esté en la dirección del desplazamiento, sólo se debe multiplicar su componente en la dirección del movimiento.
Será considerado trabajo positivo el realizado por un agente externo al sistema carga-campo que ocasione un cambio de posición y negativo aquél que realice el campo.
Teniendo en cuenta la expresión (1):
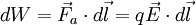
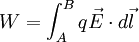
Expresándolo matemáticamente:

El trabajo infinitesimal es el producto escalar del vector fuerza F por el vector desplazamiento dl, tangente a la trayectoria, o sea:
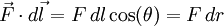
donde dr es el desplazamiento infinitesimal de la carga q en la dirección radial.
Para calcular el trabajo total, se integra entre la posición inicial A, distante del centro de fuerzas y la posición final B, distante
del centro de fuerzas y la posición final B, distante  del centro fijo de fuerzas:
del centro fijo de fuerzas:
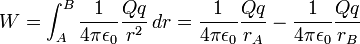
De lo anterior se concluye que el trabajo W no depende del camino seguido por la partícula para ir desde la posición A a la posición B. lo cual implica que la fuerza de atracción F, que ejerce la carga Q sobre la carga q es conservativa. La fórmula de la energía potencial es:
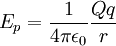
Por definición, el nivel cero de energía potencial se ha establecido en el infinito, o sea, si y sólo si  .
.
Energía Potencial
En un sistema físico, la energía potencial es energía que mide la capacidad que tiene dicho sistema para realizar un trabajo en función exclusivamente de su posición o configuración. Puede pensarse como la energía almacenada en el sistema, o como una medida del trabajo que un sistema puede entregar. Suele abreviarse con la letra o
o  .
.
La energía potencial puede presentarse como energía potencial gravitatoria, energía potencial electrostática, y energía potencial elástica.
Más rigurosamente, la energía potencial es una magnitud escalar asociada a un campo de fuerzas (o como en elasticidad un campo tensorial de tensiones). Cuando la energía potencial está asociada a un campo de fuerzas, la diferencia entre los valores del campo en dos puntos A y B es igual al trabajo realizado por la fuerza para cualquier recorrido entre B y A.
La energía potencial puede definirse solamente cuando la fuerza es conservativa. Si las fuerzas que actúan sobre un cuerpo son no conservativas, entonces no se puede definir la energía potencial, como se verá a continuación. Una fuerza es conservativa cuando se cumple alguna de las siguientes propiedades:
La forma funcional de la energía potencial depende de la fuerza de que se trate; así, para el campo gravitatorio (o eléctrico), el resultado del producto de las masas (o cargas) por una constante dividido por la distancia entre las masas (cargas), por lo que va disminuyendo a medida que se incrementa dicha distancia.
Considérese una carga puntual q en presencia de un campo eléctrico. La carga experimentará una fuerza eléctrica. Se define como el trabajo "W"
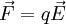
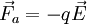 (1)
(1)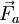 . El trabajo queda, entonces, expresado como:
. El trabajo queda, entonces, expresado como:
Será considerado trabajo positivo el realizado por un agente externo al sistema carga-campo que ocasione un cambio de posición y negativo aquél que realice el campo.
Teniendo en cuenta la expresión (1):
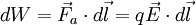
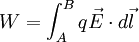
Expresándolo matemáticamente:

El trabajo infinitesimal es el producto escalar del vector fuerza F por el vector desplazamiento dl, tangente a la trayectoria, o sea:
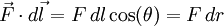
Para calcular el trabajo total, se integra entre la posición inicial A, distante
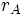 del centro de fuerzas y la posición final B, distante
del centro de fuerzas y la posición final B, distante  del centro fijo de fuerzas:
del centro fijo de fuerzas: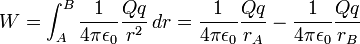
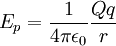
 .
.Energía Potencial
En un sistema físico, la energía potencial es energía que mide la capacidad que tiene dicho sistema para realizar un trabajo en función exclusivamente de su posición o configuración. Puede pensarse como la energía almacenada en el sistema, o como una medida del trabajo que un sistema puede entregar. Suele abreviarse con la letra
 o
o  .
.La energía potencial puede presentarse como energía potencial gravitatoria, energía potencial electrostática, y energía potencial elástica.
Más rigurosamente, la energía potencial es una magnitud escalar asociada a un campo de fuerzas (o como en elasticidad un campo tensorial de tensiones). Cuando la energía potencial está asociada a un campo de fuerzas, la diferencia entre los valores del campo en dos puntos A y B es igual al trabajo realizado por la fuerza para cualquier recorrido entre B y A.
La energía potencial puede definirse solamente cuando la fuerza es conservativa. Si las fuerzas que actúan sobre un cuerpo son no conservativas, entonces no se puede definir la energía potencial, como se verá a continuación. Una fuerza es conservativa cuando se cumple alguna de las siguientes propiedades:
- El trabajo realizado por la fuerza entre dos puntos es independiente del camino recorrido.
- El trabajo realizado por la fuerza para cualquier camino cerrado es nulo.
- Cuando el rotor de la fuerza es cero.
Si las fuerzas no son conservativas no existirá en general una manera unívoca de definir la anterior integral. De la propiedad anterior se sigue que si la energía potencial es conocida, se puede obtener la fuerza a partir del gradiente de U:
También puede recorrerse el camino inverso: suponer la existencia una función energía potencial y definir la fuerza correspondiente mediante la fórmula anterior. Se puede demostrar que toda fuerza así definida es conservativa.
La forma funcional de la energía potencial depende de la fuerza de que se trate; así, para el campo gravitatorio (o eléctrico), el resultado del producto de las masas (o cargas) por una constante dividido por la distancia entre las masas (cargas), por lo que va disminuyendo a medida que se incrementa dicha distancia.
Diferencia de Potencial eléctrico
Considérese una carga de prueba positiva  en presencia de un campo eléctrico y que se traslada desde el punto A al punto B conservándose siempre en equilibrio. Si se mide el trabajo que debe hacer el agente que mueve la carga, la diferencia de potencial eléctrico se define como:
en presencia de un campo eléctrico y que se traslada desde el punto A al punto B conservándose siempre en equilibrio. Si se mide el trabajo que debe hacer el agente que mueve la carga, la diferencia de potencial eléctrico se define como: 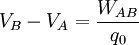
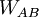 puede ser positivo, negativo o nulo. En estos casos el potencial eléctrico en B será respectivamente mayor, menor o igual que el potencial eléctrico en A. La unidad en el SI para la diferencia de potencial que se deduce de la ecuación anterior es Joule/Coulomb y se representa mediante una nueva unidad, el voltio, esto es: 1 voltio = 1 joule/coulomb.
puede ser positivo, negativo o nulo. En estos casos el potencial eléctrico en B será respectivamente mayor, menor o igual que el potencial eléctrico en A. La unidad en el SI para la diferencia de potencial que se deduce de la ecuación anterior es Joule/Coulomb y se representa mediante una nueva unidad, el voltio, esto es: 1 voltio = 1 joule/coulomb.
Un electronvoltio (eV) es la energía adquirida para un electrón al moverse a través de una diferencia de potencial de 1 V, 1 eV = 1,6x10-19 J. Algunas veces se necesitan unidades mayores de energía, y se usan los kiloelectronvoltios (keV), megaelectronvoltios (MeV) y los gigaelectronvoltios (GeV). (1 keV=103 eV, 1 MeV = 106 eV, y 1 GeV = 109 eV).
Aplicando esta definición a la teoría de circuitos y desde un punto de vista más intuitivo, se puede decir que el potencial eléctrico en un punto de un circuito representa la energía que posee cada unidad de carga al paso por dicho punto. Así, si dicha unidad de carga recorre un circuito constituyendóse en corriente eléctrica, ésta irá perdiendo su energía (potencial o voltaje) a medida que atraviesa los diferentes componentes del mismo. Obviamente, la energía perdida por cada unidad de carga se manifestará como trabajo realizado en dicho circuito (calentamiento en una resistencia, luz en una lámpara, movimiento en un motor, etc.). Por el contrario, esta energía perdida se recupera al paso por fuentes generadoras de tensión.
Es conveniente distinguir entre potencial eléctrico en un punto (energía por unidad de carga situada en ese punto) y corriente eléctrica (número de cargas que atraviesan dicho punto por segundo).
Usualmente se escoge el punto A a una gran distancia (en rigor el infinito) de toda carga y el potencial eléctrico a esta distancia infinita recibe arbitrariamente el valor cero. Esto permite definir el potencial eléctrico en un punto poniendo
a esta distancia infinita recibe arbitrariamente el valor cero. Esto permite definir el potencial eléctrico en un punto poniendo 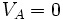 y eliminando los índices:
y eliminando los índices:
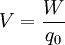
 el trabajo que debe hacer un agente exterior para mover la carga de prueba
el trabajo que debe hacer un agente exterior para mover la carga de prueba  desde el infinito al punto en cuestión.
desde el infinito al punto en cuestión.
Obsérvese que la igualdad planteada depende de que se da arbitrariamente el valor cero al potencial en la posición de referencia (el infinito) el cual hubiera podido escogerse de cualquier otro valor así como también se hubiera podido seleccionar cualquier otro punto de referencia.
en la posición de referencia (el infinito) el cual hubiera podido escogerse de cualquier otro valor así como también se hubiera podido seleccionar cualquier otro punto de referencia.
También es de hacer notar que según la expresión que define el potencial eléctrico en un punto, el potencial en un punto cercano a una carga positiva aislada es positivo porque debe hacerse trabajo positivo mediante un agente exterior para llevar al punto una carga de prueba (positiva) desde el infinito. Similarmente, el potencial cerca de una carga negativa aislada es negativo porque un agente exterior debe ejercer una fuerza (trabajo negativo en este caso) para sostener a la carga de prueba (positiva) cuando esta (la carga positiva) viene desde el infinito.
Por último, el potencial eléctrico queda definido como un escalar porque y
y  son escalares.
son escalares.
Tanto como
como 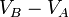 son independientes de la trayectoria que se siga al mover la carga de prueba desde el punto A hasta el punto B. Si no fuera así, el punto B no tendría un potencial eléctrico único con respecto al punto A y el concepto de potencial sería de utilidad restringida.
son independientes de la trayectoria que se siga al mover la carga de prueba desde el punto A hasta el punto B. Si no fuera así, el punto B no tendría un potencial eléctrico único con respecto al punto A y el concepto de potencial sería de utilidad restringida.
Es posible demostrar que las diferencias de potencial son independientes de la trayectoria para el caso especial representado en la figura. Para mayor simplicidad se han escogido los puntos A y B en una recta radial.
Una carga de prueba puede trasladarse desde A hacia B siguiendo la trayectoria I sobre una recta radial o la trayectoria II completamente arbitraria.
La trayectoria II puede considerarse equivalente a una trayectoria quebrada formada por secciones de arco y secciones radiales alternadas. Puesto que estas secciones se pueden hacer tan pequeñas como se desee, la trayectoria quebrada puede aproximarse a la trayectoria II tanto como se quiera. En la trayectoria II el agente externo hace trabajo solamente a lo largo de las secciones radiales, porque a lo largo de los arcos, la fuerza y el corrimiento
y el corrimiento 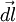 son perpendiculares y en tales casos
son perpendiculares y en tales casos 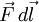 es nulo. La suma del trabajo hecho en los segmentos radiales que constituyen la trayectoria II es el mismo que el trabajo efectuado en la trayectoria I, porque cada trayectoria está compuesta del mismo conjunto de segmentos radiales. Como la trayectoria II es arbitraria, se ha demostrado que el trabajo realizado es el mismo para todas las trayectorias que unen A con B.
es nulo. La suma del trabajo hecho en los segmentos radiales que constituyen la trayectoria II es el mismo que el trabajo efectuado en la trayectoria I, porque cada trayectoria está compuesta del mismo conjunto de segmentos radiales. Como la trayectoria II es arbitraria, se ha demostrado que el trabajo realizado es el mismo para todas las trayectorias que unen A con B.
Aun cuando esta prueba sólo es válida para el caso especial ilustrado en la figura, la diferencia de potencial es independiente de la trayectoria para dos puntos cualesquiera en cualquier campo eléctrico. Se desprende de ello el carácter conservativo de la interacción electrostática el cual está asociado a la naturaleza central de las fuerzas electrostáticas.
Para un par de placas paralelas en las cuales se cumple que
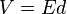 ,
,
donde d es la distancia entre las placas paralelas y E es el campo eléctrico constante en la región entre las placas.
 en presencia de un campo eléctrico y que se traslada desde el punto A al punto B conservándose siempre en equilibrio. Si se mide el trabajo que debe hacer el agente que mueve la carga, la diferencia de potencial eléctrico se define como:
en presencia de un campo eléctrico y que se traslada desde el punto A al punto B conservándose siempre en equilibrio. Si se mide el trabajo que debe hacer el agente que mueve la carga, la diferencia de potencial eléctrico se define como: 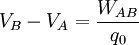
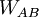 puede ser positivo, negativo o nulo. En estos casos el potencial eléctrico en B será respectivamente mayor, menor o igual que el potencial eléctrico en A. La unidad en el SI para la diferencia de potencial que se deduce de la ecuación anterior es Joule/Coulomb y se representa mediante una nueva unidad, el voltio, esto es: 1 voltio = 1 joule/coulomb.
puede ser positivo, negativo o nulo. En estos casos el potencial eléctrico en B será respectivamente mayor, menor o igual que el potencial eléctrico en A. La unidad en el SI para la diferencia de potencial que se deduce de la ecuación anterior es Joule/Coulomb y se representa mediante una nueva unidad, el voltio, esto es: 1 voltio = 1 joule/coulomb.Un electronvoltio (eV) es la energía adquirida para un electrón al moverse a través de una diferencia de potencial de 1 V, 1 eV = 1,6x10-19 J. Algunas veces se necesitan unidades mayores de energía, y se usan los kiloelectronvoltios (keV), megaelectronvoltios (MeV) y los gigaelectronvoltios (GeV). (1 keV=103 eV, 1 MeV = 106 eV, y 1 GeV = 109 eV).
Aplicando esta definición a la teoría de circuitos y desde un punto de vista más intuitivo, se puede decir que el potencial eléctrico en un punto de un circuito representa la energía que posee cada unidad de carga al paso por dicho punto. Así, si dicha unidad de carga recorre un circuito constituyendóse en corriente eléctrica, ésta irá perdiendo su energía (potencial o voltaje) a medida que atraviesa los diferentes componentes del mismo. Obviamente, la energía perdida por cada unidad de carga se manifestará como trabajo realizado en dicho circuito (calentamiento en una resistencia, luz en una lámpara, movimiento en un motor, etc.). Por el contrario, esta energía perdida se recupera al paso por fuentes generadoras de tensión.
Es conveniente distinguir entre potencial eléctrico en un punto (energía por unidad de carga situada en ese punto) y corriente eléctrica (número de cargas que atraviesan dicho punto por segundo).
Usualmente se escoge el punto A a una gran distancia (en rigor el infinito) de toda carga y el potencial eléctrico
 a esta distancia infinita recibe arbitrariamente el valor cero. Esto permite definir el potencial eléctrico en un punto poniendo
a esta distancia infinita recibe arbitrariamente el valor cero. Esto permite definir el potencial eléctrico en un punto poniendo 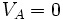 y eliminando los índices:
y eliminando los índices: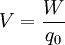
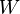 el trabajo que debe hacer un agente exterior para mover la carga de prueba
el trabajo que debe hacer un agente exterior para mover la carga de prueba  desde el infinito al punto en cuestión.
desde el infinito al punto en cuestión.Obsérvese que la igualdad planteada depende de que se da arbitrariamente el valor cero al potencial
 en la posición de referencia (el infinito) el cual hubiera podido escogerse de cualquier otro valor así como también se hubiera podido seleccionar cualquier otro punto de referencia.
en la posición de referencia (el infinito) el cual hubiera podido escogerse de cualquier otro valor así como también se hubiera podido seleccionar cualquier otro punto de referencia.También es de hacer notar que según la expresión que define el potencial eléctrico en un punto, el potencial en un punto cercano a una carga positiva aislada es positivo porque debe hacerse trabajo positivo mediante un agente exterior para llevar al punto una carga de prueba (positiva) desde el infinito. Similarmente, el potencial cerca de una carga negativa aislada es negativo porque un agente exterior debe ejercer una fuerza (trabajo negativo en este caso) para sostener a la carga de prueba (positiva) cuando esta (la carga positiva) viene desde el infinito.
Por último, el potencial eléctrico queda definido como un escalar porque
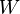 y
y  son escalares.
son escalares.Tanto
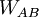 como
como 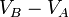 son independientes de la trayectoria que se siga al mover la carga de prueba desde el punto A hasta el punto B. Si no fuera así, el punto B no tendría un potencial eléctrico único con respecto al punto A y el concepto de potencial sería de utilidad restringida.
son independientes de la trayectoria que se siga al mover la carga de prueba desde el punto A hasta el punto B. Si no fuera así, el punto B no tendría un potencial eléctrico único con respecto al punto A y el concepto de potencial sería de utilidad restringida.Una carga de prueba puede trasladarse desde A hacia B siguiendo la trayectoria I sobre una recta radial o la trayectoria II completamente arbitraria.
La trayectoria II puede considerarse equivalente a una trayectoria quebrada formada por secciones de arco y secciones radiales alternadas. Puesto que estas secciones se pueden hacer tan pequeñas como se desee, la trayectoria quebrada puede aproximarse a la trayectoria II tanto como se quiera. En la trayectoria II el agente externo hace trabajo solamente a lo largo de las secciones radiales, porque a lo largo de los arcos, la fuerza
 y el corrimiento
y el corrimiento 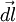 son perpendiculares y en tales casos
son perpendiculares y en tales casos 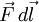 es nulo. La suma del trabajo hecho en los segmentos radiales que constituyen la trayectoria II es el mismo que el trabajo efectuado en la trayectoria I, porque cada trayectoria está compuesta del mismo conjunto de segmentos radiales. Como la trayectoria II es arbitraria, se ha demostrado que el trabajo realizado es el mismo para todas las trayectorias que unen A con B.
es nulo. La suma del trabajo hecho en los segmentos radiales que constituyen la trayectoria II es el mismo que el trabajo efectuado en la trayectoria I, porque cada trayectoria está compuesta del mismo conjunto de segmentos radiales. Como la trayectoria II es arbitraria, se ha demostrado que el trabajo realizado es el mismo para todas las trayectorias que unen A con B.Aun cuando esta prueba sólo es válida para el caso especial ilustrado en la figura, la diferencia de potencial es independiente de la trayectoria para dos puntos cualesquiera en cualquier campo eléctrico. Se desprende de ello el carácter conservativo de la interacción electrostática el cual está asociado a la naturaleza central de las fuerzas electrostáticas.
Para un par de placas paralelas en las cuales se cumple que
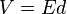 ,
, donde d es la distancia entre las placas paralelas y E es el campo eléctrico constante en la región entre las placas.
Potencial Eléctrico
El potencial eléctrico en un punto es el trabajo que debe realizar una fuerza eléctrica para mover una carga positiva q desde la referencia hasta ese punto, dividido por unidad de carga de prueba. Dicho de otra forma, es el trabajo que debe realizar una fuerza externa para traer una carga unitaria q desde la referencia hasta el punto considerado en contra de la fuerza eléctrica. Matemáticamente se expresa por:
 localizada a una distancia r de una carga q, la energía potencial electrostática mutua es:
localizada a una distancia r de una carga q, la energía potencial electrostática mutua es:
 =
= 
 localizada a una distancia r de una carga q, la energía potencial electrostática mutua es:
localizada a una distancia r de una carga q, la energía potencial electrostática mutua es: =
= 
Lineas de Campo
Líneas de campo eléctrico correspondientes a cargas iguales y opuestas, respectivamente.
Un campo eléctrico estático puede ser representado geométricamente con líneas tales que en cada punto el campo vectorial sea tangente a dichas líneas, a estas líneas se las conoce como "líneas de campo". Matemáticamente las líneas de campo son las curvas integrales del campo vectorial. Las líneas de campo se utilizan para crear una representación gráfica del campo, y pueden ser tantas como sea necesario visualizar.
Las líneas de campo son líneas perpendiculares a la superficie del cuerpo, de manera que su tangente geométrica en un punto coincide con la dirección del campo en ese punto. Esto es una consecuencia directa de la ley de Gauss, es decir encontramos que la mayor variación direccional en el campo se dirige perpendicularmente a la carga. Al unir los puntos en los que el campo eléctrico es de igual magnitud, se obtiene lo que se conoce como superficies equipotenciales, son aquellas donde el potencial tiene el mismo valor numérico. En el caso estático al ser el campo eléctrico un campo irrotacional las líneas de campo nunca serán cerradas (cosa que sí puede suceder en el caso dinámico, donde el rotacional del campo eléctrico es igual a la variación temporal del campo magnético cambiada de signo, por tanto una línea de campo eléctrico cerrado requiere un campo magnético variable, cosa imposible en el caso estático).
En el caso dinámico pueden definirse igualmente las líneas sólo que el patrón de líneas variará de un instante a otro del tiempo, es decir, las líneas de campo al igual que las cargas serán móviles.
CAMPO ELECTRICO
El campo eléctrico es un campo físico que es representado mediante un modelo que describe la interacción entre cuerpos y sistemas con propiedades de naturaleza eléctrica. Matemáticamente se describe como un campo vectorial en el cual una carga eléctrica puntual de valor q sufre los efectos de una fuerza eléctrica 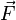 dada por la siguiente ecuación:
dada por la siguiente ecuación:
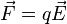
En los modelos relativistas actuales, el campo eléctrico se incorpora, junto con el campo magnético, en campo tensorial cuadridimensional, denominado campo electromagnético Fμν.[]
Los campos eléctricos pueden tener su origen tanto en cargas eléctricas como en campos magnéticos variables. Las primeras descripciones de los fenómenos eléctricos, como la ley de Coulomb, sólo tenían en cuenta las cargas eléctricas, pero las investigaciones de Michael Faraday y los estudios posteriores de James Clerk Maxwell permitieron establecer las leyes completas en las que también se tiene en cuenta la variación del campo magnético.
Esta definición general indica que el campo no es directamente medible, sino que lo que es observable es su efecto sobre alguna carga colocada en su seno. La idea de campo eléctrico fue propuesta por Faraday al demostrar el principio de inducción electromagnética en el año 1832.
La unidad del campo eléctrico en el SI es Newton por culombio (N/C), voltio por metro (V/m) o, en unidades básicas, kg·m·s−3·A−1.
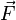 dada por la siguiente ecuación:
dada por la siguiente ecuación: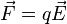
En los modelos relativistas actuales, el campo eléctrico se incorpora, junto con el campo magnético, en campo tensorial cuadridimensional, denominado campo electromagnético Fμν.[]
Los campos eléctricos pueden tener su origen tanto en cargas eléctricas como en campos magnéticos variables. Las primeras descripciones de los fenómenos eléctricos, como la ley de Coulomb, sólo tenían en cuenta las cargas eléctricas, pero las investigaciones de Michael Faraday y los estudios posteriores de James Clerk Maxwell permitieron establecer las leyes completas en las que también se tiene en cuenta la variación del campo magnético.
Esta definición general indica que el campo no es directamente medible, sino que lo que es observable es su efecto sobre alguna carga colocada en su seno. La idea de campo eléctrico fue propuesta por Faraday al demostrar el principio de inducción electromagnética en el año 1832.
La unidad del campo eléctrico en el SI es Newton por culombio (N/C), voltio por metro (V/m) o, en unidades básicas, kg·m·s−3·A−1.
Constante dieléctrica
La constante dieléctrica o permitividad relativa de un medio continuo es una propiedad macroscópica de un medio dieléctrico relacionado con la permitividad eléctrica del medio.
en relación la rapidez de las ondas electromagnéticas en un dieléctrico es:
El nombre proviene de los materiales dieléctricos, que son materiales aislantes o muy poco conductores por debajo de una cierta tensión eléctrica llamada tensión de rotura. El efecto de la constante dieléctrica se manifiesta en la capacidad total de un condensador eléctrico o capacitor. Cuando entre los conductores cargados o paredes que lo forman se inserta un material dieléctrico diferente del aire (cuya permitividad es prácticamente la del vacío) la capacidad de almacenamiento de la carga del condensador aumenta. De hecho la relación entre la capacidad inicial Ci y la final Cf vienen dada por la constante eléctrica:
Donde ε es la permitividad eléctrica del dieléctrico que se inserta.
Además el valor de la constante dieléctrica K de un material define el grado de polarización eléctrica de la substancia cuando esta se somete a un campo eléctrico exterior. El valor de K es afectado por muchos factores, como el peso molecular, la forma de la molécula, la dirección de sus enlaces (geometría de la molécula) o el tipo de interacciones que presente.
Cuando un material dieléctrico remplaza el vacío entre los conductores, puede presentarse la polarización en el dieléctrico, permitiendo que se almacenen cargas adicionales.
Vacio---------------1.0
Aire----------------1.004
SiO2 ------------3.9
Papel--------------4-6
Al2-------------5.9
TiO3------------100
BaTiO3----------1500
PMN ---------------->10000
Pb(Mg1/3 Nb2/3)O3
en relación la rapidez de las ondas electromagnéticas en un dieléctrico es:
donde k es la constante dieléctrica y km es la permeabilidad relativa
El nombre proviene de los materiales dieléctricos, que son materiales aislantes o muy poco conductores por debajo de una cierta tensión eléctrica llamada tensión de rotura. El efecto de la constante dieléctrica se manifiesta en la capacidad total de un condensador eléctrico o capacitor. Cuando entre los conductores cargados o paredes que lo forman se inserta un material dieléctrico diferente del aire (cuya permitividad es prácticamente la del vacío) la capacidad de almacenamiento de la carga del condensador aumenta. De hecho la relación entre la capacidad inicial Ci y la final Cf vienen dada por la constante eléctrica:
Donde ε es la permitividad eléctrica del dieléctrico que se inserta.
Además el valor de la constante dieléctrica K de un material define el grado de polarización eléctrica de la substancia cuando esta se somete a un campo eléctrico exterior. El valor de K es afectado por muchos factores, como el peso molecular, la forma de la molécula, la dirección de sus enlaces (geometría de la molécula) o el tipo de interacciones que presente.
Cuando un material dieléctrico remplaza el vacío entre los conductores, puede presentarse la polarización en el dieléctrico, permitiendo que se almacenen cargas adicionales.
La magnitud de la carga que se puede almacenar entre los conductores se conoce como capacitancia ésta depende de la constante dieléctrica del material existente entre los conductores, el tamaño, la forma y la separación de los mismos.
La constante dieléctrica puede ser medida de la siguiente manera, primero medimos la capacidad de un capacitor de prueba en el vacío Ci (o en aire si aceptamos un pequeño error), luego usando el mismo capacitor y la misma distancia entre sus placas se mide la capacidad con el dieléctrico insertado entre ellas Cf.
La constante dieléctrica puede ser calculada como:
- K para diferentes materiales
Vacio---------------1.0
Aire----------------1.004
SiO2 ------------3.9
Papel--------------4-6
Al2-------------5.9
TiO3------------100
BaTiO3----------1500
PMN ---------------->10000
Pb(Mg1/3 Nb2/3)O3
Suscribirse a:
Comentarios (Atom)