Considérese una carga puntual q en presencia de un campo eléctrico. La carga experimentará una fuerza eléctrica. Se define como el trabajo "W"
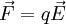
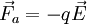 (1)
(1)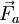 . El trabajo queda, entonces, expresado como:
. El trabajo queda, entonces, expresado como:
Será considerado trabajo positivo el realizado por un agente externo al sistema carga-campo que ocasione un cambio de posición y negativo aquél que realice el campo.
Teniendo en cuenta la expresión (1):
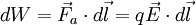
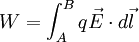
Expresándolo matemáticamente:

El trabajo infinitesimal es el producto escalar del vector fuerza F por el vector desplazamiento dl, tangente a la trayectoria, o sea:
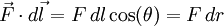
Para calcular el trabajo total, se integra entre la posición inicial A, distante
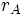 del centro de fuerzas y la posición final B, distante
del centro de fuerzas y la posición final B, distante  del centro fijo de fuerzas:
del centro fijo de fuerzas: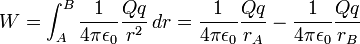
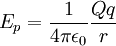
 .
.Energía Potencial
En un sistema físico, la energía potencial es energía que mide la capacidad que tiene dicho sistema para realizar un trabajo en función exclusivamente de su posición o configuración. Puede pensarse como la energía almacenada en el sistema, o como una medida del trabajo que un sistema puede entregar. Suele abreviarse con la letra
 o
o  .
.La energía potencial puede presentarse como energía potencial gravitatoria, energía potencial electrostática, y energía potencial elástica.
Más rigurosamente, la energía potencial es una magnitud escalar asociada a un campo de fuerzas (o como en elasticidad un campo tensorial de tensiones). Cuando la energía potencial está asociada a un campo de fuerzas, la diferencia entre los valores del campo en dos puntos A y B es igual al trabajo realizado por la fuerza para cualquier recorrido entre B y A.
La energía potencial puede definirse solamente cuando la fuerza es conservativa. Si las fuerzas que actúan sobre un cuerpo son no conservativas, entonces no se puede definir la energía potencial, como se verá a continuación. Una fuerza es conservativa cuando se cumple alguna de las siguientes propiedades:
- El trabajo realizado por la fuerza entre dos puntos es independiente del camino recorrido.
- El trabajo realizado por la fuerza para cualquier camino cerrado es nulo.
- Cuando el rotor de la fuerza es cero.
Si las fuerzas no son conservativas no existirá en general una manera unívoca de definir la anterior integral. De la propiedad anterior se sigue que si la energía potencial es conocida, se puede obtener la fuerza a partir del gradiente de U:
También puede recorrerse el camino inverso: suponer la existencia una función energía potencial y definir la fuerza correspondiente mediante la fórmula anterior. Se puede demostrar que toda fuerza así definida es conservativa.
La forma funcional de la energía potencial depende de la fuerza de que se trate; así, para el campo gravitatorio (o eléctrico), el resultado del producto de las masas (o cargas) por una constante dividido por la distancia entre las masas (cargas), por lo que va disminuyendo a medida que se incrementa dicha distancia.


No hay comentarios:
Publicar un comentario